将来の価値から一定の利子率で割引くことにより求めた現在価値をいいます。
現価計数とは
将来価値から現在価値を求めるための計数です。
この係数を使うことによって、割引現在価値は将来価値に乗ずるだけで求めることができます。
割引現在価値=将来価値×現価計数
年金現価計数とは
一定期間ごとに一定額を支払または受取続ける場合に、将来価値から現在価値の合計を求めるための計数です。
現在で、割引現在価値が採用されているものは、
・減損が生じた固定資産
・リースの資産と債務
・利息法の償却原価法で評価する社債
・退職給付債務
・資産除去債務
があります。
割引現在価値
割引現在価値を身近な例で考えてみましょう。
3年後に発売される100万円の欲しい車があり、現時点でお金を使わないように定期預金で預けるとします。
しかし、100万円を預けることはないのです。定期預金はご存知のように利子が付きます。
そのため、現在いくらを定期預金で預ければ3年後に100万円になるかを計算してみましょう。
利子率は1%の固定金利とし、利子にかかる所得税は考えないものとします。
1,000,000÷1.01³(1,000,000÷1.01÷1.01÷1.01)で970,590円になります。
すなわち、970,590円を定期預金に預ければいいわけです。
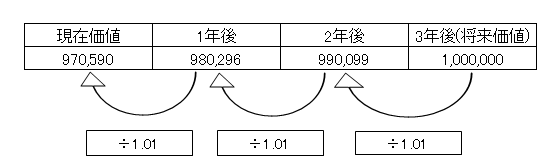
これを割引現在価値で言い直せば、3年後に得られる1,000,000円の現在価値は970,590円となります。
現価計数
割引現在価値の項目の例を、下記の現価計数からもとめてみます。
5年後を基準にしているのでそこから3年前だと現価計数は0,97059となります。
1,000,000×0.97059=970,590円となり同額になりました。

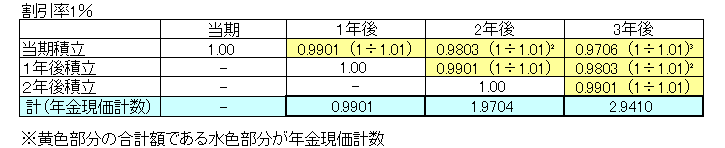
年金現価計数
例として、1年ごとに1,000円ずつ3年間もらえるようにする場合の、割引現在価値を求めます。
利子率は1%の固定金利とし、利子にかかる所得税は考えないものとします。
3年後の金額を年利1%で割引いた割引現在価値を求めると、下記の図から年金現価計数は2.9410となります。
1,000(毎月積立額)×2.9410(年金現価計数)=2,941
となります。
2,941円の元手で毎年1,000円ずつ受け取れるか検証してみましょう。
検証図は下記のようになり受取が可能なことがわかります。
このように年金現価計数を用いることで計算できます。
.png)